
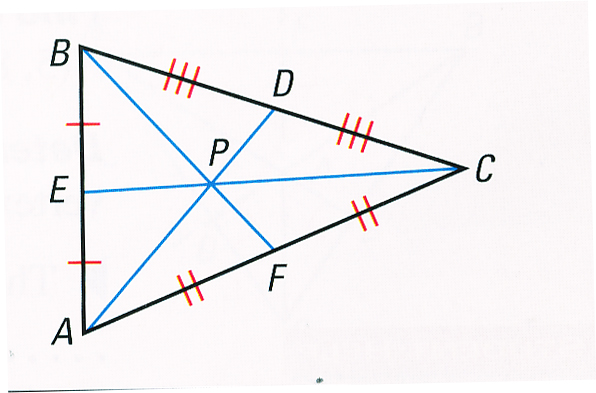
Mark the largest angle and longest side in red and the smallest angle and shortest side in blue. In Exercises 9 and 10, use a ruler and protractor to draw the given type of triangle. If ∠X and ∠Y are less than 30, then m∠X + m∠Y is not equal to 62. (B) Both ∠X and ∠Y have measures less than 30°.ī and C. (A) Both ∠X and ∠Y have measures greater than 20°. In Exercises 7 and 8, determine which two statements contradict each other. The slope of the given line is \(\frac \) is a median. Write an equation of the line passing through point P that is perpendicular to the given line. Relationships Within Triangles Maintaining Mathematical Proficiency
Exercise 6.5 Indirect Proof and Inequalities in One Triangle – Page(340-342).Lesson 6.5 Indirect Proof and Inequalities in One Triangle – Page(336-342).6.5 Indirect Proof and Inequalities in One Triangle –.Exercise 6.4 The Triangle Midsegment Theorem – Page(333-334).Lesson 6.4 The Triangle Midsegment Theorem – Page (330-334).6.4 The Triangle Midsegment Theorem –.Exercise 6.3 Medians and Altitudes of Triangles – Page(324-326).Lesson 6.3 Medians and Altitudes of Triangles – Page(320-326).6.3 Medians and Altitudes of Triangles –.Exercise 6.2 Bisectors of Triangles – Page(315-318).
Lesson 6.2 Bisectors of Triangles – Page(310-318).Exercise 6.1 Perpendicular And Angle Bisectors – Page(306-308).Lesson 6.1 Perpendicular And Angle Bisectors – Page(302-308).6.1 Perpendicular And Angle Bisectors –.Relationships Within Triangles Mathematical Practices –.Relationships Within Triangles Maintaining Mathematical Proficiency –.So, here are the links to access Topic-wise Big Ideas Math Geometry Answers Chapter 6 Relationships Within Triangles & ace up your preparation.
#ALTITUDE GEOMETRY DEF HOW TO#
Students who need to learn how to Answer Ch 6 Relationships Within Triangles Questions should definitely go ahead with this page and score maximum marks in the exams. All the questions covered in this study material is very beneficial for students to understand the concept thoroughly. Improve your subject knowledge & clear all your exams with flying colors by taking the help of the BIM Geometry solution key of Ch 6 Relationships Within Triangles. Big Ideas Math Book Geometry Answer Key Chapter 6 Relationships Within Triangles
#ALTITUDE GEOMETRY DEF FOR FREE#
All you can attain for free of cost and make use of this Ch 6 Relationships Within Triangles Big Ideas Math Geometry Answers for better practice and learning. This BIM Geometry Solution key covered all Chapter 6 Relationships Within Triangles Exercises Questions, Practices, Chapter Review, Chapter Test, Assessments, etc. The apothem of a regular polygon is also the height of an isosceles triangle formed by the center and a side of the polygon, as shown in the figure below.įor the regular pentagon ABCDE above, the height of isosceles triangle BCG is an apothem of the polygon.Need instant homework help for solving all chapter 6 Relationships Within Triangles Questions? Then, don’t worry we have come up with a great study guide and one-stop destination for looking at what you require ie., Big Ideas Math Geometry Answers Chapter 6 Relationships Within Triangles. The length of the base, called the hypotenuse of the triangle, is times the length of its leg. When the base angles of an isosceles triangle are 45°, the triangle is a special triangle called a 45°-45°-90° triangle. Base BC reflects onto itself when reflecting across the altitude. Leg AB reflects across altitude AD to leg AC. The altitude of an isosceles triangle is also a line of symmetry.
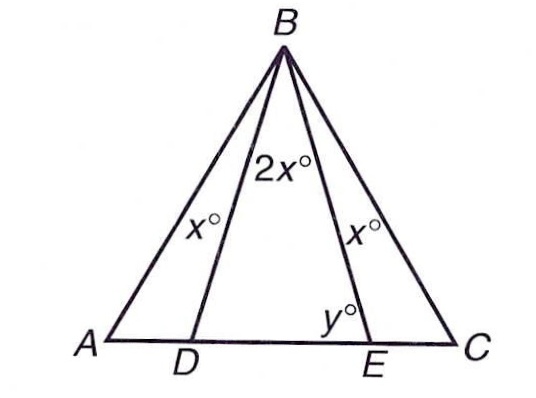
So, ∠B≅∠C, since corresponding parts of congruent triangles are also congruent. Based on this, △ADB≅△ADC by the Side-Side-Side theorem for congruent triangles since BD ≅CD, AB ≅ AC, and AD ≅AD. Using the Pythagorean Theorem where l is the length of the legs. ABC can be divided into two congruent triangles by drawing line segment AD, which is also the height of triangle ABC. Refer to triangle ABC below.ĪB ≅AC so triangle ABC is isosceles. The base angles of an isosceles triangle are the same in measure. Using the Pythagorean Theorem, we can find that the base, legs, and height of an isosceles triangle have the following relationships: The height of an isosceles triangle is the perpendicular line segment drawn from base of the triangle to the opposing vertex. The angle opposite the base is called the vertex angle, and the angles opposite the legs are called base angles. Parts of an isosceles triangleįor an isosceles triangle with only two congruent sides, the congruent sides are called legs. DE≅DF≅EF, so △DEF is both an isosceles and an equilateral triangle.


 0 kommentar(er)
0 kommentar(er)
